In questa pagina si riportano 10 esercizi svolti su alcune delle tipologie più complesse di quiz di Matematica e Fisica presenti nei Test di Medicina dell'Università San Raffaele.
Quiz n. 1
Traccia:
Quanto vale la somma dei numeri pari da 6 a 80?
a) 1428
b) 1677
c) 1634
d) 1365
e) 1720
Risoluzione:
La formula per determinare la somma dei numeri pari è la seguente:
Spari = [n • (a1 + an)] / 2
dove "n" è il numero dei termini da sommare; "a1" è il valore del primo termine e "an" è il valore dell'ennesimo termine.
I numeri pari da "2" a "80" sono 40, infatti, pochè vi è un numero pari ogni due numeri, basta dimezzare il numero "80" (N.B.: ai fini del conteggio non si prende in considerazione lo "0" dato che il suo valore non influisce in una sommatoria).
Nel caso in esame i termini da sommare sono 38; vanno infatti sottratti il "2" e il "4" perchè non compresi tra "6" e "80".
Si applica pertanto la formula sopra indicata tenendo presente che a1 = 6 e an = 80:
Spari = [38 • (6 + 80)] / 2
⇓
Spari = (38 • 86) / 2
⇓
Spari = 19 • 86
⇓
Spari = 1634
La risposta corretta è, quindi, la c).
Quiz n. 2
Traccia:
Ricercare il numero intero x che è soluzione della seguente equazione: 6•(x-1)! - 2•(x+1)! = -3•x!
a) 2
b) 2/3
c) 4
d) 9
e) 6
Risoluzione:
Il fattoriale di un numero è uguale al prodotto di tutti i numeri naturali (escluso lo zero) minori o uguali a tale numero. Pertanto, x! è dato da:
x! = x • (x-1) • (x-2) • ... • 1
E' possibile anche esprimere x! nel seguente modo:
x! = x • (x-1)!
In maniera analoga anche (x+1)! può essere espresso in funzione di (x-1)!; si ha infatti:
(x+1)! = (x+1) • x • (x-1)!
Sostituendo i valori appena ricavati di x! e (x+1)! nell'equazione data, si ottiene:
6•(x-1)! - 2•(x+1)•x•(x-1)! = -3•x•(x-1)!
Dividendo tutti i termini dell'equazione per (x-1)!, si ha:
6 - 2•(x+1)•x = -3•x
⇓
6 - 2x2 - 2x = -3x
⇓
2x2 - x - 6 = 0
⇓
x1/2 = (-b ± √Δ) / 2a = (1 ± 7) / 4
⇓
x1 = -3/2 (non intero) e x2 = 2
La risposta corretta è, quindi, la a).
Quiz n. 3
Traccia:
Determinare il valore di k per cui la retta y = 2x + 1 è tangente alla circonferenza x2 + y2 = k - 1.
a) per k = -3/2
b) per k = 6/5
c) per k = 1/2
d) per k = -5/6
e) nessuna delle altre alternative proposte
Risoluzione:
Per determinare algebricamente le intersezioni tra una retta e una circonferenza si possono mettere a sistema le relative equazioni; si ottiene, in tal modo, un'equazione risolutiva di II grado che permette di determinare il numero di intersezioni (pari al numero di soluzioni dell'equazione) tra retta e circonferenza.
Si possono presentare 3 casi:
- se Δ > 0 si hanno 2 soluzioni dell'equazione e quindi la retta interseca la circonferenza in 2 punti (retta secante);
- se Δ = 0 si ha un'unica soluzione dell'equazione (2 soluzioni coincidenti) e quindi la retta interseca la circonferenza in un punto (retta tangente);
- se Δ < 0 non si hanno soluzioni dell'equazione e quindi non vi sono punti di intersezione tra retta e circonferenza (retta esterna).
Pertanto, mettendo a sistema le equazioni date, si ha:
x2 + (2x+1)2 = k - 1
⇓
x2 + 4x2 + 4x + 1 = k - 1
⇓
5x2 + 4x + 2 - k = 0
⇓
Δ = 16 - 20•(2-k) = 20k - 24
Ponendo la condizione di tangenza Δ = 0, si ottiene:
20k - 24 = 0
⇓
k = 6/5
La risposta corretta è, quindi, la b).
Quiz n. 4
Traccia:
Quanto vale la somma dei primi cinque termini della progressione geometrica di ragione 4 e il cui primo termine vale 2?
a) 400
b) 1364
c) 124
d) 312
e) 682
Risoluzione:
La somma dei primi "n" numeri in una progressione geometrica, di ragione q e con primo elemento a1, è data dalla seguente formula:
Sn = a1 • [(1-qn) / (1-q)]
⇓
Sn = 2 • [(1-45) / (1-4)]
⇓
Sn = 2 • 341
⇓
Sn = 682
La risposta corretta è, quindi, la e).
LEZIONI PRIVATE ONLINE CON L'ING. GALEONE
Ti stai preparando per il Test Medicina all'Università San Raffaele?
Affidati alla professionalità e all'esperienza...prenota ora la tua lezione privata online con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Per maggiori info clicca QUI.
Quiz n. 5
Traccia:
Il dominio della funzione f(x) = [ln(x+1)] / (x-2) è uguale a:
a) (1, +∞)
b) (-1, +∞)
c) (0, +∞)
d) (-1, 2) U (2, +∞)
e) nessuna delle alternative proposte
Risoluzione:
Per calcolare il dominio o campo di esistenza della funzione f(x) devono essere verificate le seguenti 2 condizioni:
1) essendo f(x) una funzione razionale, bisogna imporre, per l'esistenza della stessa, che il denominatore sia diverso da zero:
x-2 ≠ 0
⇓
x ≠ 2
2) bisogna, inoltre, imporre per l'esistenza del logaritmo, che il suo argomento sia maggiore di zero:
x+1 > 0
⇓
x > -1
Dalle 2 condizioni appena imposte, si deduce che il dominio della funzione è costituito da tutti i numeri reali maggiori di -1 ad esclusione del numero 2:
(-1, 2) U (2, +∞)
La risposta corretta è, quindi, la d).
Quiz n. 6
Traccia:
Un gas perfetto alla temperatura di –173 °C è contenuto, alla pressione di 1 atm, in un recipiente di volume pari a 2 m3. Se il volume del recipiente si dimezza e se la pressione del gas diventa pari a 4 atm, quale sarà la sua temperatura finale?
a) la temperatura rimane costante
b) 200 K
c) 519 °C
d) 27 °C
e) 73 °C
Risoluzione:
Per il gas perfetto in esame deve valere l'equazione di stato sia nello stato iniziale che nello stato finale.
Nello stato finale si ha:
p2•V2 = n•R•T2
dove "n" è il numero di moli e "R" è la costante universale dei gas.
Per ricavare la temperatura finale, si utilizza la formula inversa:
T2 = (p2•V2) / (n•R)
Nella relazione appena scritta p2 e V2 sono noti; per ricavare il prodotto (n•R), si può applicare l'equazione di stato dei gas perfetti anche nello stato iniziale:
p1•V1 = n•R•T1
⇓
n•R = (p1•V1) / T1
⇓
n•R = (1•105 [Pa] • 2 [m3]) / 100 [K]
⇓
n•R = 2•103 [(Pa • m3) / K]
Pertanto, si può ricavare la temperatura finale:
T2 = (p2•V2) / (n•R)
⇓
T2= (4•105 [Pa] • 1 [m3]) / 2•103 [(Pa • m3) / K]
⇓
T2 = 200 K
La risposta corretta è, quindi, la b).
Quiz n. 7
Traccia:
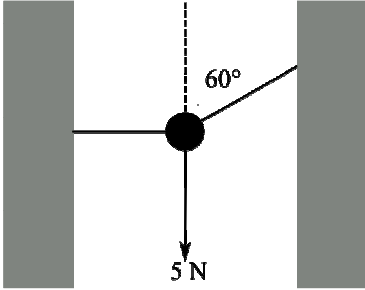
Un corpo di peso 5 N è tenuto in equilibrio da due corde di massa trascurabile, come mostrato in figura. Una delle due corde crea un angolo di 60° con la verticale che punta verso l’alto, mentre l’altra corda è orizzontale. Qual è il valore della tensione della corda orizzontale?
a) 10√3 N
b) 5√3 N
c) 1,25√3 N
d) 5 N
e) 10 N
Risoluzione:
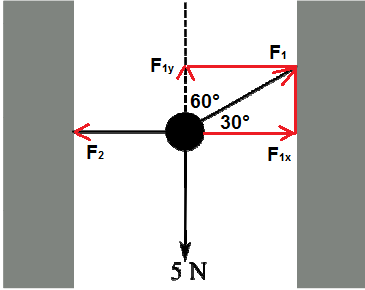
Con riferimento alla figura sottostante, la forza peso di 5 N del corpo deve essere equilibrata da una forza che ha la stessa intensità (F1y = 5 N), la stessa direzione e verso opposto.
La forza F1y non è altro che la componente verticale della forza F1 esercitata dalla prima corda; dal primo teorema sui triangoli rettangoli si ha:
F1y = F1 • cos(60°)
⇓
F1 = F1y / (1/2)
F1 = 10 N
Affinchè vi sia equilibrio alla traslazione anche lungo l'asse x, la tensione della seconda corda dovrà avere la stessa intensità della componente orizzontale della tensione della prima corda (stessa direzione e verso opposto):
F2 = F1x = F1 • cos(30°)
⇓
F2 = 10 • (√3/2)
F2 = 5√3 N
La risposta corretta è, quindi, la b).
Quiz n. 8
Traccia:
Una ciclista accelera uniformemente a partire da una velocità iniziale di 3,0 m/s fino a raggiungere in 4,0 secondi una velocità finale di 5,0 m/s. Successivamente mantiene questa velocità per altri 6,0 secondi. Quale distanza è stata percorsa dalla ciclista durante i 10 secondi?
a) 31 m
b) 34 m
c) 62 m
d) 38 m
e) 46 m
Risoluzione:
Nella prima parte del percorso il ciclista si muove di moto rettilineo uniformemente accelerato; la sua accelerazione può essere ricavata dal rapporto tra la variazione di velocità e il tempo in cui tale variazione è avvenuta:
a = (vf - vi)/t
⇓
a = (5 - 3) / 4
a = 0,5 m/(s2)
Lo spazio percorso in questa prima parte di tragitto si ricava dalla seguente legge oraria:
s1 = v0•t + (1/2)•a•t2
⇓
s1 = [3•4 + (1/2)•0,5•42] m
⇓
s1 = 16 m
Nella seconda parte del tragitto il ciclista si muove di moto rettilineo uniforme alla velocità di 5 m/s, quindi nei restanti 6 secondi percorrerà:
s2 = v•t
⇓
s2 = 5•6
s2 = 30 m
Il ciclista ha pertanto percorso, in 10 secondi, la seguente distanza totale:
s = s1 + s2 = 16 + 30 = 46 m
La risposta corretta è, quindi, la e).
Quiz n. 9
Traccia:
Un blocco di polistirene ha un volume di 600 ml. Quale volume del blocco si trova al di sopra del liquido quando il blocco galleggia nel tetracloruro di carbonio? [densità del polistirene = 1060 kg/m3; densità del tetracloruro di carbonio = 1590 kg/m3]
a) 200 ml
b) 0 ml
c) 0,20 ml
d) 0,40 ml
e) 400 ml
Risoluzione:
Quando il blocco galleggia (condizione di equilibrio) la spinta di Archimede esercitata dal tetracloruro di carbonio sul blocco di polistirene è uguale alla forza peso del blocco stesso.
La spinta di Archimede vale:
dove df è la densità del fluido, g è l'accelerazione di gravità e Vf è il volume immerso (volume del fluido spostato dal blocco di polistirene).
La forza peso del blocco vale: Fpeso = m•g = dc•Vc•g, dove dc è la densità del corpo immerso e Vc il suo volume.
Uguagliando le due relazioni appena ottenute si ottiene il volume immerso del blocco:
S = Fpeso
⇓
⇓
Vf = (dc / df) • Vc
⇓
Vf = [(1060 / 1590) • 600] ml
Vf = 400 ml
Si può infine ricavare il volume incognito "Vx" del blocco al di sopra del liquido:
Vx = Vc - Vf
⇓
Vx = (600 - 400) ml
Vx = 200 ml
La risposta corretta è, quindi, la a).
Quiz n. 10
Traccia:
Una noce di cocco di massa 1 kg cade da un'altezza di 10 metri. Se viene trascurato l'attrito con l'aria, con quale energia, approssimativamente, la noce colpisce il suolo?
a) 100 N
b) 980 J
c) 10 N
d) 100 J
e) 10 J
Risoluzione:
Nello stato iniziale la noce di cocco, di massa "m = 1 kg", è ferma all'altezza "h = 10 m":
- la sua energia cinetica [(1/2)•m•v2] è nulla perchè la sua velocità (v) è pari a 0 m/s;
- la sua energia potenziale (m•g•h) ha valore massimo pari a (1 kg)•[10 m/(s2)]•(10 m) = 100 J [N.B.: il valore numerico 9,81 m/(s2) dell'accelerazione di gravità è stato approssimato a 10 m/(s2)];
- energia meccanica complessiva = energia cinetica + energia potenziale = 0 J + 100 J = 100 J.
Nello stato finale, ossia quando la noce di cocco raggiunge il suolo, per il principio di conservazione dell'energia, tutta l'energia potenziale si è trasformata in energia cinetica; la sua energia meccanica complessiva è comunque rimasta invariata: 100 J.
(N.B.: al suolo l'energia cinetica è massima perché massima è la velocità della noce di cocco; l'energia potenziale è nulla perché l'altezza vale 0 metri)
La risposta corretta è, quindi, la d).
LEZIONI PRIVATE ONLINE CON L'ING. GALEONE
Ti stai preparando per il Test Medicina all'Università San Raffaele?
Affidati alla professionalità e all'esperienza...prenota ora la tua lezione privata online con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Per maggiori info clicca QUI.
Torna alla pagina principale:
Test Medicina San Raffaele