In questa pagina si riportano 15 quiz svolti di Ragionamento Logico e Problemi presenti nelle Banche Dati relative al TOLC MED 2024-25 e nei test di ammissione ufficiali alla Facoltà di Medicina e Chirurgia degli ultimi anni
Quiz n. 1 (n. 7 Banca Dati Ragionamento Logico e Problemi - TOLC MED Prima Sessione 2024)
Traccia:
Cinque amici (Marcello, Leonardo, Giacomo, Alessandro e Federico) sono gli unici componenti di un equipaggio di canottaggio. L'imbarcazione è dotata di cinque posti disposti in fila uno dietro all'altro. Si sa che nella fila Federico siede tre posti indietro rispetto a Giacomo che, però, non è il primo della fila, mentre Marcello siede tre posti avanti rispetto a Leonardo. In base alle precedenti affermazioni si può dedurre che:
a) Giacomo è seduto subito dietro Alessandro
b) Leonardo è seduto nell'ultimo posto della fila
c) Giacomo è seduto nel primo posto della fila
d) Alessandro è seduto subito dietro Marcello
e) Alessandro è seduto subito dietro Giacomo
Risoluzione:
Nell'imbarcazione, Federico siede tre posti indietro rispetto a Giacomo; secondo questa ipotesi, le uniche configurazioni possibili sono: Giacomo (1° posto) - Federico (4° posto) oppure Giacomo (2° posto) - Federico (5° posto). Poichè Giacomo non è il primo della fila, la seconda configurazione è quella corretta.
Inoltre Marcello siede tre posti avanti rispetto a Leonardo, quindi le uniche configurazioni possibili sono: Marcello (1° posto) - Leonardo (4° posto) oppure Marcello (2° posto) - Leonardo (5° posto). Ovviamente l'unica configurazione corretta è la prima, dato che il 2° e il 4° posto sono già occupati da Giacomo e Federico.
Per esclusione, Alessandro siede al 3° posto dell'imbarcazione.
La risposta corretta è, quindi, la e), infatti Alessandro è seduto subito dietro Giacomo.
Quiz n. 2 (n. 62 Banca Dati Ragionamento Logico e Problemi - TOLC MED Prima Sessione 2024)
Traccia:
Alice apre la cabina armadio e conta le scatole delle sue scarpe.
• Se divide il numero delle scatole per 2 le rimane il resto di 1.
• Se divide per 3 nessun resto.
• Se divide per 5 le rimane il resto di 4.
Sapendo che il numero delle scatole è maggiore di 4 e minore di 45, quante sono le possibili soluzioni al problema di determinare il numero delle scatole di scarpe di Alice?
a) 2
b) 4
c) 0
d) 1
e) 8
Risoluzione:
Si deve ricercare un numero naturale compreso tra 5 e 44 (estremi inclusi) che rispetta le 3 condizioni date.
Dalla prima condizione, si deduce che il numero di scatole non è divisibile per 2, quindi è dispari; si escludono, quindi, tutti i numeri pari presenti nell'intervallo sopra indicato.
La seconda condizione suggerisce, invece, che il numero incognito deve essere divisibile per 3.
In base alle due considerazioni appena fatte, il numero di scatole deve essere scelto tra i seguenti:
9, 15, 21, 27, 33, 39
L'ultima condizione indica che, dividendo il numero incognito per 5, rimane un resto di 4.
Dividendo i sei numeri rimasti per 5, si ottengono i seguenti resti:
9:5 ⇒ resto 4
15:5 ⇒ resto 0
21:5 ⇒ resto 1
27:5 ⇒ resto 2
33:5 ⇒ resto 3
39:5 ⇒ resto 4
Pertanto, le possibili soluzioni al problema sono 2, il numero 9 e il numero 39.
La risposta corretta è, quindi, la a).
Quiz n. 3 (n. 68 Banca Dati Ragionamento Logico e Problemi - TOLC MED Prima Sessione 2024)
Traccia:
Quattro numeri naturali a, b, c, d sono tali che a < b < c < d. A quale dei quattro numeri Enea deve sommare 1 in modo che il prodotto dei tre numeri inalterati con quello modificato sia il più piccolo possibile?
a) a
b) c
c) d
d) è indifferente, in ogni caso si ottiene sempre la stessa variazione
e) b
Risoluzione:
Si considerano i 4 prodotti possibili aggiungendo "1" rispettivamente ad "a", quindi a "b", poi a "c" ed infine a "d":
1° caso: (a+1) • bcd = abcd + bcd
2° caso: (b+1) • acd = abcd + acd
3° caso: (c+1) • abd = abcd + abd
4° caso: (d+1) • abc = abcd + abc
In tutti e 4 i casi esaminati, i risultati hanno in comune il termine "abcd" che, quindi, non è determinante nella ricerca del prodotto più piccolo possibile.
Il termine decisivo è, invece, il prodotto dei 3 numeri rimasti inalterati che risulta essere minimo nel 4° caso, in quanto "abc" è il prodotto dei 3 numeri più piccoli (a<b<c<d).
In conclusione, il prodotto più piccolo si ottiene aggiungendo "1" a "d", cioè al numero più grande:
(d+1) • abc = abcd + abc
La risposta corretta è, quindi, la c).
Quiz n. 4 (n. 247 Banca Dati Ragionamento Logico e Problemi - TOLC MED Prima Sessione 2024)
Traccia:
I 700 seggi di un parlamento sono ripartiti fra 10 partiti politici. Non ci sono due partiti con uno stesso numero di seggi e ciascun partito ha almeno 10 seggi. Qual è il più alto numero di seggi che il quinto partito può avere?
a) 130
b) 126
c) 14
d) 128
e) 131
Risoluzione:
Poichè si ricerca il più alto numero di seggi che il 5° partito può avere, si determina dapprima il minimo numero di seggi che possono essere assegnati ai partiti classificatisi dal 6° al 10° posto, tenendo conto che non possono esserci 2 partiti con lo stesso numero di seggi e ciascun partito ha almeno 10 seggi:
7° partito: 13 seggi
8° partito: 12 seggi
9° partito: 11 seggi
I seggi rimanenti da assegnare ai primi 5 partiti diventano di conseguenza:
Si indica con "x" il numero massimo di seggi che possono essere assegnati al 5° partito; il numero minimo di seggi che devono essere assegnati ai primi 4 partiti si ottiene aggiungendo in successione 1 seggio, 2 seggi, 3 seggi e 4 seggi al numero "x" dei seggi del 5° partito:
2° partito: "x+3"
3° partito: "x+2"
4° partito: "x+1"
E' possibile impostare, infine, una semplice equazione di I grado nell'incognita "x", ricordando che la somma dei seggi assegnabili ai primi 5 partiti è stata determinata precedentemente e vale 640:
⇓
5x = 640 - 10
⇓
5x = 630
⇓
x = 126
La risposta corretta è, quindi, la b).
TOLC MED 2024-25 - LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il TOLC MED 2024-25?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Quiz n. 5 (n. 2 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2021-2022)
Traccia:
Tre insiemi A, B, C contengono ciascuno 4 elementi; se A ∩ B ∩ C contiene 1 elemento, 1 elemento appartiene solo a C e il numero di elementi che appartengono solo a A è 1 in più del numero di elementi che appartengono solo a B in quanti modi, mediante i diagrammi di Venn, si possono visualizzare i tre insiemi?
a) 2
b) 3
c) 4
d) 1
e) 0
Risoluzione:
Si utilizzano i diagrammi di Venn per rappresentare innanzitutto i dati certi forniti dalla traccia del quiz:
- nell'intersezione dei 3 insiemi (A ∩ B ∩ C) vi è 1 solo elemento;
- inoltre, vi è 1 solo elemento che appartiene solo all'insieme C.
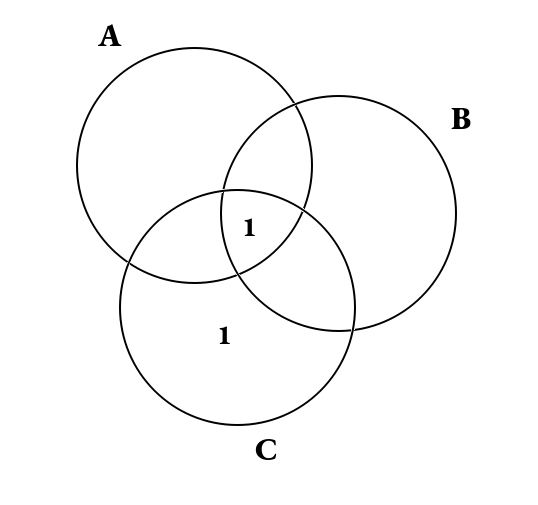
Successivamente, si tiene conto del fatto che l'insieme A (così come gli altri due insiemi) deve avere al suo interno 4 elementi.
Poichè, però, l'elemento inserito nell'intersezione dei 3 insiemi appartiene anche ad A, si deduce che gli elementi che appartengono solo ad A possono essere 1, 2 o 3, altrimenti si supererebbero i 4 elementi previsti.
(N.B. gli elementi che appartengono ad A non possono essere 0, in quanto la traccia afferma che il numero di elementi che appartengono solo ad A sono 1 in più rispetto a quelli che appartengono solo a B)
Proprio per la nota sopra indicata, se gli elementi che appartengono ad A possono essere 1, 2 o 3, allora quelli che appartengono solo a B possono essere solo 0, 1 o 2 (cioè 1 in meno).
In base alle considerazioni precedenti, si rappresentano gli unici 3 casi possibili:
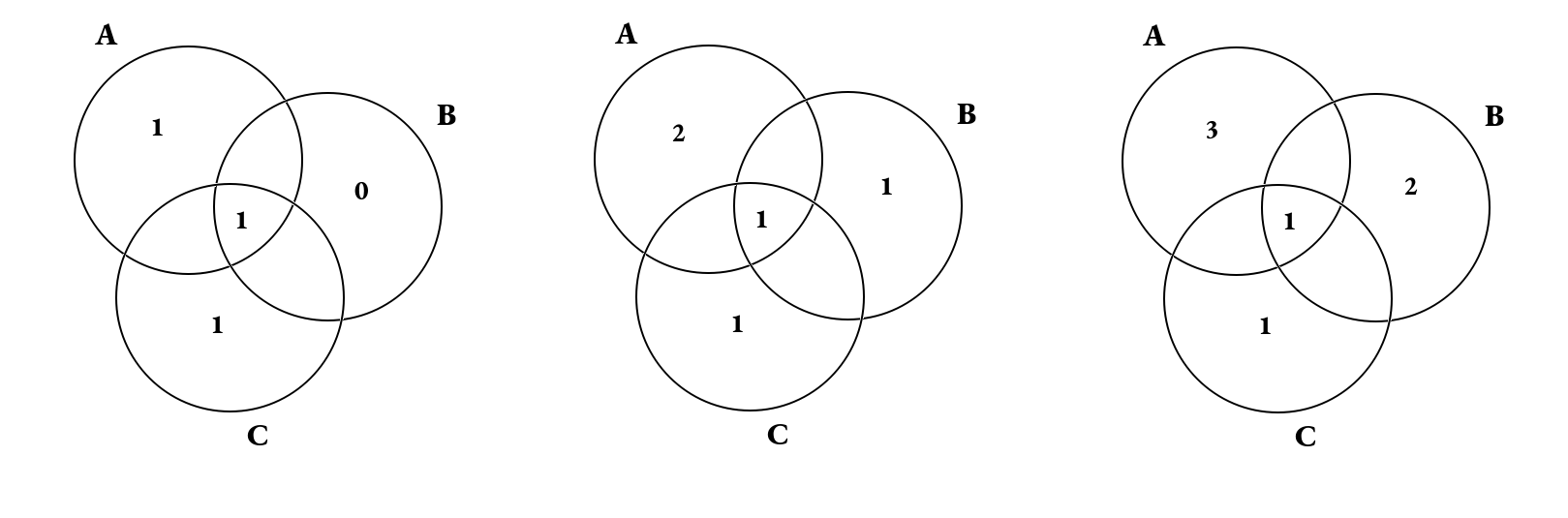
Se si cercano poi di riempire le intersezioni A ∩ B, A ∩ C e B ∩ C, si nota che nessuna combinazione permette di ottenere un numero esatto di 4 elementi per tutti e 3 gli insiemi.
La risposta corretta è, quindi, la e).
Quiz n. 6 (n. 21 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2020-2021)
Traccia:
Il formato carta indica la dimensione (lunghezza e larghezza) di un foglio di carta. Lo standard internazionale del formato carta, l’ISO 216, prevede un rapporto pari a 2 fra lunghezza e larghezza del foglio. Il formato iniziale è denominato A0, i successivi formati (A1, A2, A3, ...) si ottengono sempre dividendo a metà il formato precedente lungo il lato più lungo. Riferendosi alla lunghezza iniziale LU e alla larghezza iniziale LA del formato A0 a quale delle seguenti frazioni corrisponde la lunghezza del formato A4?
a) LA/4
b) LU/4
c) LA/2
d) LU/8
e) LA/8
Risoluzione:
Il formato A1 si ottiene da quello A0 dividendo a metà il suo lato più lungo, mentre si mantiene inalterata l'altra dimensione del rettangolo; pertanto, si deduce che l'area del foglio A1 è pari alla metà di quella del foglio A0.
Ragionando in modo simile con i formati successivi all'A1, si ha che:
- l'area del formato A2 è la metà di quello A1
- l'area del formato A3 è la metà di quello A2
- l'area del formato A4 è la metà di quello A3
In definitiva, l'area del foglio A4 è pari a 1/16 dell'area del foglio A0; indicando allora con "LU" ed "LA" le dimensioni del formato A0 e con "LU4" ed "LA4" quelle del formato A4, si ha:
LU4 • LA4 = (1/16) • (LU • LA)
Poichè, per qualsiasi formato, il rapporto tra lunghezza e larghezza è sempre pari a √2, dalla relazione precedente si ottiene:
LU4 • (LU4/√2) = (1/16) • [LU • (LU/√2)]
⇓
LU42 / √2 = LU2 / 16√2
⇓
LU42 = LU2 / 16
⇓
LU4 = LU / 4
La risposta corretta è, quindi, la b).
Quiz n. 7 (n. 19 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2020-2021)
Traccia:
L’oro lavorato possiede il 75% di oro mentre la parte rimanente è presentata da alcuni metalli che permettono di aumentarne la rigidità e variarne il colore. La gioielleria di Tommaso è famosa per gli anelli in oro verde realizzato con il 12,5% di rame e il 12,5% di argento. Se Tommaso ha in magazzino 12 g di argento, 28 g di rame e 60 g di oro, quanti grammi di oro verde può realizzare al massimo?
a) 74
b) 96
c) 72
d) 88
e) 80
Risoluzione:
Il quiz propone un problema sul cosiddetto "massimo vincolato".
Infatti, si deve ricercare il massimo valore in grammi di oro verde che si riesce a realizzare tenendo conto dei vincoli imposti sui tre metalli che lo costituiscono (oro, argento e rame): singole percentuali di composizione dell'oro verde e grammi a disposizione.
Se il 75% dell'oro verde è costituito da oro, vuol dire che il peso dell'oro è pari ai 3/4 di quello dell'oro verde; quindi, con 60 grammi a disposizione di oro, si riescono a realizzare al massimo:
60 • (4/3) = 80 g di oro verde
In maniera analoga, se il 12,5% dell'oro verde è costituito da rame, significa che il peso del rame è pari ai 1/8 di quello dell'oro verde; pertanto, con 28 grammi a disposizione di rame, si riescono a realizzare al massimo:
28 • 8 = 224 g di oro verde
Infine, se il 12,5% dell'oro verde è costituito da argento, vuol dire che il peso dell'argento è pari ai 1/8 di quello dell'oro verde; quindi, con 12 grammi a disposizione di argento, si riescono a realizzare al massimo:
12 • 8 = 96 g di oro verde
Si deduce che Tommaso può realizzare al massimo 80 g di oro verde, infatti, se volesse realizzare anche solo un grammo in più di oro verde, non avrebbe oro a sufficienza (pur avendo ancora discrete quantità di rame ed argento a disposizione).
La risposta corretta è, pertanto, la e).
Quiz n. 8 (n. 22 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2020-2021)
Traccia:
Definito nell’insieme dei numeri reali l’operatore ◊ dalla relazione a ◊ b = ab – a – b, qual è il valore dell’espressione (a ◊ b) ◊ c – (a ◊ c) ◊ b?
a) a - 2ac
b) a + bc
c) 2b - 2c
d) 2c + ab
e) b + 2c
Risoluzione:
Tenendo conto della relazione "a ◊ b = ab – a – b" che definisce come debba essere applicato l'operatore "◊", si calcola innanzitutto il primo termine "(a ◊ b) ◊ c" dell'espressione richiesta:
a ◊ b = ab - a - b
⇓
(a ◊ b) ◊ c = (ab - a - b) ◊ c =
= abc - ac - bc - ab + a + b - c
Successivamente, si ricava il secondo termine "(a ◊ c) ◊ b" dell'espressione:
a ◊ c = ac - a - c
⇓
(a ◊ c) ◊ b = (ac - a - c) ◊ b =
= abc - ab - bc - ac + a + c - b
Infine, si calcola il valore della differenza "(a ◊ b) ◊ c – (a ◊ c) ◊ b":
(a ◊ b) ◊ c – (a ◊ c) ◊ b = (ac - a - c) ◊ b =
= abc - ac - bc - ab + a + b - c - abc + ab + bc + ac - a - c + b
⇓
(a ◊ b) ◊ c – (a ◊ c) ◊ b = 2b - 2c
La risposta corretta è, quindi, la c).
Quiz n. 9 (n. 7 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2019-2020)
Traccia:
Per il suo acquario Michele ha acquistato 50 pesci fra neon, guppy, black angel e clown loach. 46 non sono guppy, 33 non sono clown loach e i neon sono uno in più dei black angel. Quanti sono i neon?
a) 15
b) 11
c) 12
d) 14
e) 13
Risoluzione:
Si indicano con "n", "g", "ba" e "cl" il numero rispettivamente di pesci neon, guppy, black angel e clown loach.
Se 46 pesci non sono guppy, per differenza si può ricavare il numero dei pesci guppy acquistati:
g = 50-46 = 4
In modo analogo, se 33 pesci non sono clown loach, si ottiene il numero dei pesci clown loach acquistati:
cl = 50-33 = 17
Infine, si possono scrivere le due seguenti relazioni, conoscendo la somma dei pesci neon e dei pesci black angel e sapendo che i neon sono uno in più rispetto ai black angel:
Sostituendo il valore di "n", ricavato dalla relazione 2), nella relazione 1), si ottiene il numero di pesci black angel:
1) ba + 1 + ba = 29
⇓
2•ba = 28
⇓
ba = 14
Infine, sostituendo il valore di "ba" appena calcolato nella relazione 2), si ricava il numero dei pesci neon:
2) n = 14 + 1 = 15
La risposta corretta è, quindi, la a).
Quiz n. 10 (n. 8 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2019-2020)
Traccia:
In un negozio di giocattoli Alice trova dei peluche di topo Gigio di due dimensioni, quelli grandi costano il doppio di quelli piccoli. Alice decide di acquistarne cinque piccoli e tre grandi. Se, al contrario, avesse acquistato cinque peluche grandi e tre piccoli, avrebbe speso 24 € in più. Qual è il prezzo che Alice paga per un topo Gigio grande?
a) 6 €
b) 18 €
c) 9 €
d) 12 €
e) 24 €
Risoluzione:
Si indica con "x" il costo del peluche di topo Gigio piccolo e con "2x" il costo del peluche di topo Gigio grande.
Alice ha acquistato 5 peluche piccoli e 3 grandi, spendendo effettivamente:
5•x + 3•(2x) = 11•x
Mentre, se Alice avesse acquistato 5 peluche grandi e 3 piccoli, avrebbe speso ipoteticamente:
La spesa ipotetica di Alice, afferma la traccia del quiz, supera di 24 € quella effettiva; pertanto, impostando la seguente equazione di I grado, si può ricavare il costo "2x" del peluche di topo Gigio grande:
13•x = 11•x + 24
⇓
2•x = 24 €
La risposta corretta è, quindi, la e).
Quiz n. 11 (n. 15 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2018-2019)
Traccia:
Giorgio deve trasferirsi per lavoro a Milano; preso in affitto un appartamento si reca presso gli uffici dell’azienda alpha per la stipula di un contratto per la fornitura dell’energia elettrica. Allo sportello il dipendente dell’azienda gli propone tre tipi di tariffe:
- tariffa A: un costo fisso di 40 € mensili e 0,3 € ogni 5 kwh di energia consumati;
- tariffa B: un costo fisso di 30 € mensili e 0.4 € ogni 5 kwh di energia consumati;
- tariffa C: 0,6 € ogni 5 kwh di energia consumati.
Se nel precedente appartamento il consumo medio di energia di Giorgio era di 600 kwh, quale/i delle tre tariffe risulta/no più conveniente/i per Giorgio?
a) la tariffa B
b) la tariffa A
c) le tariffe A e B
d) le tariffe B e C
e) la tariffa C
Risoluzione:
In base al consumo medio di energia elettrica di Giorgio (600 kWh), si calcolano gli importi che egli dovrebbe pagare applicando le tariffe proposte:
- tariffa A: 40 € + [(600 kWh)/(5 kWh)]•0,3 € = 40 € + 120•0,3 € = 40 € + 36 € = 76 €
- tariffa B: 30 € + [(600 kWh)/(5 kWh)]•0,4 € = 30 € + 120•0,4 € = 30 € + 48 € = 78 €
- tariffa C: [(600 kWh)/(5 kWh)]•0,6 € = 120•0,6 € = 72 €
La tariffa C è quindi quella più conveniente per Giorgio: la risposta corretta è la e).
Quiz n. 12 (n. 15 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2018-2019)
Traccia:
Se l’enunciato “Se continui a gridare, perderai la voce” vale [A → B] e l’enunciato “Non risolverai il problema” vale [~ C], allora l’enunciato “Se continui a gridare, non solo non risolverai il problema, ma perderai la voce” vale:
a) [A → [[~ C] Λ B]]
b) [A → [~ [~ C] Λ B]]
c) [A → [[~ C] Λ (~B)]]
d) [A → [[~ C] → B]]
e) [A → [[~ C] Λ [~B]]
Risoluzione:
Si cerca innanzitutto di capire la corrispondenza tra i simboli e gli enunciati proposti dalla traccia del quiz:
- primo enunciato: "Se continui a gridare" = A; allora = →; "perderai la voce" = B.
N.B.: il termine "allora" è sottinteso ed intuibile in base alla presenza della virgola ed al significato dell'enunciato nel suo complesso.
- secondo enunciato: "Non" = ~; "risolverai il problema" = C.
In base a tali corrispondenze, bisogna quindi tradurre in simboli il terzo enunciato proposto, tenendo conto che il simbolo "Λ" presente nelle alternative di risposta equivale alla congiunzione "e":
"Se continui a gridare" = A; allora = →; "non" = ~; "risolverai il problema" = C; "e" = Λ; "perderai la voce" = B.
N.B.: anche in questo enunciato il termine "allora" è sottinteso ed intubile in base alla presenza della virgola ed al significato dell'enunciato nel suo complesso.
Inoltre, la congiunzione "e" sostituisce perfettamente le espressioni "non solo ...., ma ...", infatti l'enunciato vuole esprimere questo concetto: "Se si continua a gridare, le conseguenze negative sono due: non si risolve il problema per cui si grida e si perde anche la voce".
La risposta corretta è, quindi, la a):
[A → [[~ C] Λ B]]
Quiz n. 13 (n. 10 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2018-2019)
Traccia:
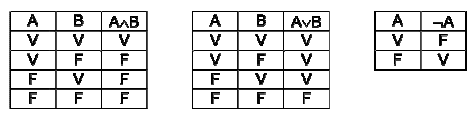
Le tavole di verità sono tabelle usate nella logica per determinare se, attribuiti i valori di verità alle proposizioni che la compongono, una determinata proposizione è vera o falsa. Le tabelle di verità della congiunzione “e” (∧), della disgiunzione “o” (∨) e della negazione “non” (¬) sono rispettivamente:
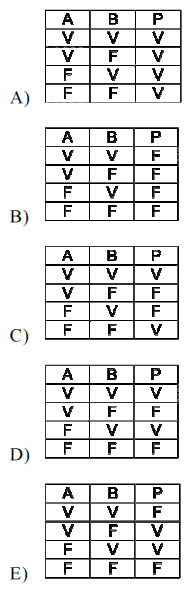
Qual è la tabella di verità della proposizione: P: ¬ (A∧B) ∨ A?
Risoluzione:
Si analizzano le singole alternative di risposta, tenendo presente che la proposizione "P: ¬ (A∧B) ∨ A" è vera se almeno una delle due seguenti condizioni è verificata (vedi "tabella di verità A∨ B" fornita dalla traccia del quiz):
1) "non (A∧B)" è vera;
2) "A" è vera.
risposta A):
- prima riga: "A" e "B" sono vere → dalla prima riga della "tabella A∧B" si ha che "A∧B" è vera, quindi "non (A∧B)" è falsa → poichè "non (A∧B)" è falsa e "A" è vera → dalla terza riga della "tabella A∨B" si ha che "P" è vera. La prima riga è quindi corretta.
- seconda riga: "A" è vera e "B" è falsa → dalla seconda riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è vera → dalla prima riga della "tabella A∨B" si ha che "P" è vera. La seconda riga è quindi corretta.
- terza riga: "A" è falsa e "B" è vera → dalla terza riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è falsa → dalla seconda riga della "tabella A∨B" si ha che "P" è vera. La terza riga è quindi corretta.
- quarta riga: "A" e "B" sono false → dalla quarta riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è falsa → dalla seconda riga della "tabella A∨B" si ha che "P" è vera. La quarta riga è quindi corretta.
La risposta A) è, quindi, quella corretta.
Per chiarire ancora meglio il ragionamento seguito, si analizza anche un'alternativa di risposta non corretta.
risposta C):
- prima riga: "A" e "B" sono vere → dalla prima riga della "tabella A∧B" si ha che "A∧B" è vera, quindi "non (A∧B)" è falsa → poichè "non (A∧B)" è falsa e "A" è vera → dalla terza riga della "tabella A∨B" si ha che "P" è vera. La prima riga è quindi corretta.
- seconda riga: "A" è vera e "B" è falsa → dalla seconda riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è vera → dalla prima riga della "tabella A∨B" si ha che "P" è vera. La seconda riga non è quindi corretta.
- terza riga: "A" è falsa e "B" è vera → dalla terza riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è falsa → dalla seconda riga della "tabella A∨B" si ha che "P" è vera. La terza riga non è quindi corretta.
- quarta riga: "A" e "B" sono false → dalla quarta riga della "tabella A∧B" si ha che "A∧B" è falsa, quindi "non (A∧B)" è vera → poichè "non (A∧B)" è vera e "A" è falsa → dalla seconda riga della "tabella A∨B" si ha che "P" è vera. La quarta riga è quindi corretta.
Quiz n. 14 (n. 8 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2017-2018)
Traccia:
Assumendo che ogni pappagallo mangi la stessa quantità di cibo ogni giorno e che lo stesso avvenga per ogni canarino, ogni giorno con 14 grammi di becchime si sfamano 4 pappagalli e 3 canarini, mentre con 18 grammi dello stesso mangime si sfamano 4 pappagalli e 5 canarini. Quale delle seguenti affermazioni NON è vera?
a) Due pappagalli e sei canarini richiedono ogni giorno lo stesso becchime di cinque pappagalli
b) Un canarino viene sfamato per 2 giorni con 4 grammi di becchime
c) Cinque pappagalli e cinque canarini richiedono ogni giorno 20 grammi di becchime
d) Un pappagallo ogni giorno mangia quanto un canarino
e) Tre pappagalli e tre canarini richiedono ogni giorno 12 grammi di becchime
Risoluzione:
Si indicano con "p" e "c" le quantità di becchime in grammi che consumano quotidianamente rispettivamente i pappagalli e i canarini; in base alle informazioni fornite dalla traccia del quesito, si può quindi impostare il seguente sistema di 2 equazioni nelle incognite "p" e "c":
2) 4p + 5c = 18
Sottraendo membro a membro i termini delle 2 equazioni si ottiene il valore di "c":
⇓
-2c = -4
⇓
c = 2
Sostituendo il valore ricavato per "c", ad esempio nella prima equazione, si ricava il valore di "p":
⇓
4p = 8
⇓
p = 2
Dai calcoli appena effettuati, si deduce che i pappagalli e i canarini giornalmente consumano 2 grammi di becchime: risultano quindi vere le alternative di risposta b), c), d) ed e); l'unica alternativa di risposta non vera è la a), infatti 2 pappagalli e 6 canarini necessitano ogni giorno di 16 grammi (= 2•2 + 6•2) di becchime, mentre 5 pappagalli hanno bisogno quotidianamente di 10 grammi (= 5•2) di becchime.
Quiz n. 15 (n. 9 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2017-2018)
Traccia:
Stephanie deve raggiungere i colleghi che partecipano a un meeting in una località inglese. Giunta all'aeroporto di Londra decide di prendere a noleggio una macchina. La benzina in Inghilterra costa 3 sterline al gallone. Si sa che:
- l'aeroporto e la località da raggiungere distano tra loro 375 km,
- ogni gallone equivale a 3,75 litri di benzina,
- una sterlina vale 1,25 euro,
- la macchina consuma 1 litro di benzina ogni 25 km.
Quale sarà la spesa sostenuta da Stephanie per la benzina necessaria per il viaggio di andata e ritorno?
a) 15 euro
b) 10 euro
c) 40 euro
d) 35 euro
e) 30 euro
Risoluzione:
Si calcolano innanzitutto i litri di benzina necessari per percorrere la distanza aeroporto-località inglese (andata e ritorno):
Si determina ora la quantità di benzina necessaria espressa in galloni:
Il valore in sterline degli 8 galloni è il seguente:
Si trasforma, quindi, l'importo di 24 sterline in euro:
La risposta corretta è, quindi, la e).
TOLC MED 2024-25 - LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il TOLC MED 2024-25?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Torna alla pagina principale Test Medicina - facoltà statali