In questa pagina si riportano 15 quiz svolti di Matematica presenti nelle Banche Dati relative al TOLC MED 2024-25 e nei test di ammissione ufficiali alla Facoltà di Medicina e Chirurgia degli ultimi anni
Quiz n. 1 (n. 9 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Siano dati due triangoli rettangoli simili. Se il primo ha cateti di lunghezza 3 e 4 cm, e il secondo ha area pari al quadruplo dell'area del primo, qual è la lunghezza dell'ipotenusa del secondo triangolo?
a) 10 cm
b) 5 cm
c) 20 cm
d) 16 cm
e) 12 cm
Risoluzione:
Le aree di due poligoni simili stanno fra loro come i quadrati di due lati omologhi. Indicando con "A1" ed "i1" l'area e l'ipotenusa del primo triangolo e con "A2" ed "i2" l'area e l'ipotenusa del secondo triangolo, si può quindi scrivere la seguente relazione:
Poichè l'area del secondo triangolo è il quadruplo dell'area del primo, si ha:
Si può inoltre ricavare il valore dell'ipotenusa del primo triangolo tramite il teorema di Pitagora:
Sostituendo i valori ottenuti di "A2" e "i1" nella prima relazione, si ottiene il valore dell'ipotenusa del secondo triangolo:
La risposta corretta è, quindi, la a).
Quiz n. 2 (n. 11 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
La retta passante per il punto (1, –1) e ortogonale alla retta di equazione 2x + y + 6 = 0 ha equazione:
a) y + 2x - 1 = 0
b) 2y - x - 3 = 0
c) 2y - x + 3 = 0
d) y - 2x + 1 = 0
e) x + y - 3 = 0
Risoluzione:
Si scrive dapprima il fascio di rette proprio di centro (1; -1):
Il coefficiente angolare incognito "m" deve essere l'antireciproco del coefficiente angolare della retta di equazione 2x + y + 6 = 0; infatti per due rette perpendicolari, di coefficienti angolari rispettivamente m ed m', vale la seguente relazione:
Il coefficiente angolare della retta 2x + y + 6 = 0 vale:
⇓
Si può quindi calcolare il coefficiente angolare "m":
Sostituendo il valore di "m" ottenuto nel fascio proprio si ottiene l'equazione della retta incognita:
La risposta corretta è, quindi, la c).
Quiz n. 3 (n. 63 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Per rappresentare il grafico di equazione 4x2 - y2 = 0, cosa si deve disegnare?
a) una parabola
b) una circonferenza
c) un'iperbole
d) una coppia di rette
e) un'ellisse
Risoluzione:
L'equazione proposta dalla traccia del quiz non si può ricondurre all'equazione canonica di un'iperbole perchè al secondo membro è presente "0" e non "1".
Invece, si può scomporre il binomio 4x2 - y2 utilizzando la formula del calcolo letterale relativa alla differenza di quadrati:
⇓
(4x - y)(4x + y) = 0
Applicando poi la legge di annullamento del prodotto, si ottengo le equazioni di due rette in forma implicita:
⇓
4x - y = 0 e 4x + y = 0
La risposta corretta è, quindi, la d).
Quiz n. 4 (n. 68 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Quali sono le soluzioni reali della disequazione Ιx-1Ι < ΙxΙ ?
a) x<0 o x>1/2
b) x>0
c) x>1/2
d) x≠0
e) x<1/2
Risoluzione:
Si studiano inizialmente i segni degli argomenti dei due valori assoluti:
x-1 ≥ 0 ⇒ x ≥ 1
x ≥ 0
Si disegna la tabella dei segni:
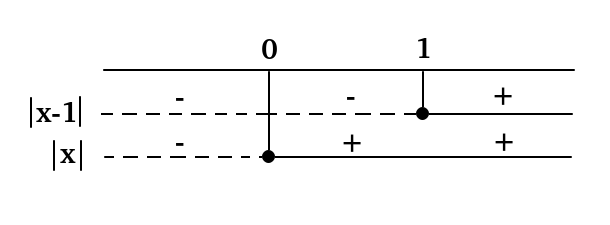
Nell'intervallo x≤0 entrambi gli argomenti dei valori assoluti sono negativi; si può risolvere, quindi, il seguente sistema:
⇓
⇓
Nell'intervallo 0<x<1 l'argomento del primo valore assoluto è negativo, mentre quello del secondo valore assoluto è positivo; pertanto, si può risolvere il seguente sistema:
⇓
⇓
⇓
Nell'intervallo x≥1 entrambi gli argomenti dei valori assoluti sono positivi; si può risolvere, quindi, il seguente sistema:
⇓
⇓
Infine, dall'unione delle soluzioni del secondo e del terzo sistema, si ricava:
⇓
Pertanto, la risposta corretta è la c).
Quiz n. 5 (n. 114 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Calcolare il valore della seguente frazione: (1272 - 732) / 2.
a) 1458
b) 10800
c) 20000
d) 5400
e) 10000
Risoluzione:
Il numeratore della frazione è una differenza di quadrati e, come tale, può trasformarsi nel prodotto somma per differenza:
= (127+73)•(127-73) =
= 200•54 = 10800
Tale numeratore va ovviamente dimezzato:
La risposta corretta è, quindi, la d).
Quiz n. 6 (n. 161 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Michele ha nel suo cassetto complessivamente 10 paia di calze, alcune a righe, altre a pois o a scacchi. Scegliendo a caso un paio di calze dal cassetto, la probabilità che trovi un paio di calze a righe è 0.4 e la probabilità che trovi un paio di calze a pois è doppia di quella che trovi un paio di calze a scacchi. Qual è la probabilità che estraendo un paio di calze dal cassetto Michele trovi quelle a scacchi?
a) 1/5
b) 2/5
c) 3/5
d) 4/5
e) 0
Risoluzione:
Indicando con P(E) la probabilità che accada l'evento E, la probabilità che si verifichi l'evento contrario P(Ē) si calcola come segue:
N.B.: la probabilità dell'evento contrario ad E equivale alla probabilità che non si verifichi E.
E' nota la probabilità che Michele estragga dal suo cassetto un paio di calze a righe: P(righe) = 0.4. Di conseguenza, tramite la formula precedente, si può calcolare la probabilità dell'evento contrario ossia che Michele estragga un paio di calze a pois o un paio di calze a scacchi:
Inoltre, poichè la probabilità che Michele trovi un paio di calze a pois è doppia rispetto a quella che trovi un paio di calze a scacchi, si può risolvere il seguente sistema:
Sostituendo il valore di P(pois), ricavato dalla relazione [1], nella relazione [2], si ricava la probabilità incognita:
Quiz n. 7 (n. 162 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Quale tra le seguenti espressioni di K rende vera l'identità sin4α - cos4α = K?
a) K = cos4α
b) K = -cos2α
c) K = cos2α
d) K = sin4α
e) K = -cos4α
Risoluzione:
Si procede al calcolo di K dapprima scomponendo il binomio sin4α - cos4α tramite la formula del calcolo letterale relativa alla differenza di quadrati:
⇓
K = (sin2α - cos2α)(sin2α + cos2α)
Poichè sin2α + cos2α = 1 (identità fondamentale della goniometria), si ottiene:
Infine, dato che cos2α = cos2α - sin2α (formula di duplicazione del coseno), si ricava:
K = -cos2α
La risposta corretta è, quindi, la b).
TOLC MED 2024-25 - LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il TOLC MED 2024-25?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Quiz n. 8 (n. 162 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Un gruppo di 10 ciclisti è composto da 6 uomini e 4 donne. I 10 ciclisti pesano in media 74 kg. Il peso medio dei 6 uomini è 82 kg. Quanto pesano in media le 4 donne?
a) 63 kg
b) 64,5 kg
c) 62 kg
d) 66 kg
e) 72 kg
Risoluzione:
Per risolvere il quesito si può applicare la formula della media aritmetica ponderata.
Si indica con "Pm" il peso medio dei 10 ciclisti, con "Pu" il peso medio dei soli uomini e con "Pd" il peso medio incognito delle sole donne.
Quindi, indicando con "u" il numero degli uomini e con "d" il numero delle donne, si ha:
Sostituendo i dati forniti dalla traccia si ottiene:
La risposta corretta è, quindi, la c).
Quiz n. 9 (n. 371 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Un triangolo rettangolo ha i cateti che misurano 10 m e 24 m. Qual è la misura della mediana relativa all’ipotenusa?
a) 12 m
b) 15 m
c) 16 m
d) 13 m
e) 26 m
Risoluzione:
In un triangolo rettangolo la mediana (segmento che congiunge un vertice con il punto medio del lato opposto) relativa all'ipotenusa è congruente a metà ipotenusa.
Utilizzando il teorema di Pitagora, si calcola l'ipotenusa del triangolo rettangolo:
Si ricava quindi il valore della mediana relativa all'ipotenusa:
La risposta corretta è, quindi, la d).
Quiz n. 10 (n. 571 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
La probabilità con cui un paziente deve attendere meno di dieci minuti il proprio turno in un ambulatorio medico è 0,8. Qual è la probabilità che una paziente che si reca due volte presso l’ambulatorio medico attenda, almeno una delle due volte, meno di dieci minuti prima di essere ricevuta dal medico?
a) 0,96
b) 0,25
c) 0,64
d) 0,04
e) 0,8
Risoluzione:
Nel calcolo della probabilità richiesto si possono avere 4 possibili combinazioni di eventi.
Si indica con "a" l'evento "attendo meno di dieci minuti" e con "b" l'evento "attendo più di dieci minuti".
Recandosi 2 volte in laboratorio i casi possibili sono 4, schematizzabili con le lettere nel seguente modo: 1) a-a; 2) a-b; 3) b-a; 4) b-b.
Indicando la probabilità che si attenda meno di 10 minuti con P(a) = 0,8 e quella che si attenda più di 10 minuti con P(b) = 0,2, le probabilità correlate ai 4 casi sopra elencati sono le seguenti:
P2 = 0,8•0,2 = 0,16
P3 = 0,2•0,8 = 0,16
P4 = 0,2•0,2 = 0,04
La probabilità che almeno una delle due volte l'attesa duri meno di 10 minuti è pari alla somma delle probabilità che avvengano i primi 3 casi possibili (in cui è presente almeno una volta l'evento "a"). Si ha quindi:
La risposta corretta è, quindi, la a).
Quiz n. 11 (n. 597 Banca Dati Fisica e Matematica - TOLC MED Prima Sessione 2024)
Traccia:
Si consideri un triangolo rettangolo isoscele con l’ipotenusa di lunghezza h cm e area di S cm quadrati. Quale tra le seguenti esprime la corretta relazione tra h ed S?
a) h = (2√2)•S
b) h = 2√S
c) h = √S/2
d) h = √(2S)
e) h = √(S/2)
Risoluzione:
Un triangolo rettangolo isoscele ha i due cateti uguali e un angolo retto, quindi è equivalente alla metà di un quadrato, di cui l'ipotenusa ne costituisce la diagonale.
Indicando con "l" i cateti e con "i" l'ipotenusa del triangolo si hanno quindi le 2 relazioni:
2) S = l2/2
⇓
l = √(2S)
Andando a sostituire il valore di "l" ottenuto dalla seconda relazione nella prima, si ha:
⇓
⇓
h = 2√S
La risposta corretta è, quindi, la b).
Quiz n. 12 (n. 55 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2021-2022)
Traccia:
Per quali valori del parametro reale k, l'equazione x2 + y2 - 4x + 2y + k = 0 rappresenta l'equazione di una circonferenza reale non degenere?
a) k<20
b) k≤ 5
c) k<5
d) k≤20
e) per ogni valore reale di k
Risoluzione:
La circonferenza degenera in un punto (coincidente con il suo centro) se il suo raggio si annulla.
Pertanto, affinchè l'equazione della circonferenza proposta non sia degenere, bisogna imporre la condizione che il raggio "r" sia maggiore di zero:
Data l'equazione canonica di una circonferenza x2 + y2 + ax + by + c = 0, la formula per ricavare il raggio è la seguente:
Nel caso in esame il raggio vale:
r = √(4 + 1 - k)
Infine, imponendo che tale valore del raggio sia positivo, si ha:
5 - k > 0
La risposta corretta è, quindi, la c).
Quiz n. 13 (n. 53 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2021-2022)
Traccia:
Qual è l'insieme delle soluzioni della disequazione 3ex - 5e-x - 2 > 0 ?
a) x∈R tale che x>ln(5/3)
b) x∈R tale che x<-1 e x>5/3
c) x∈R tale che -1<x≤ln(5/3)
d) ogni x reale
e) nessun valore di x reale
Risoluzione:
Si risolve la disequazione esponenziale proposta:
⇓
3ex - 5/ex - 2 > 0
Per semplificare i calcoli, si effettua la sostituzione di ex con un parametro generico "t":
⇓
3t2 - 2t - 5 > 0
Si risolve poi l'equazione associata per ricavare le due radici della disequazione:
Δ = 4+60 = 64
Le soluzioni della disequazione rispetto al parametro "t" sono le seguenti:
Infine, sostituendo il parametro "t" con ex, si ottiene:
ex > 5/3 ⇒ x > ln(5/3)
La risposta corretta è, quindi, la a).
Quiz n. 14 (n. 60 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2018-2019)
Traccia:
Se a = ln(4), b = ln(1/16), c = ln(8), qual è il valore dell'espressione (a-c)/b?
a) 1/4
b) -1/2
c) 1
d) -1/4
e) 1/2
Risoluzione:
Il logaritmo di una potenza è uguale al prodotto tra l'esponente della potenza e il logaritmo della base della potenza; si ha infatti:
Applicando tale formula ai dati forniti dalla traccia del quiz, si ottiene:
b = ln(1/16) = ln(2-4) = -4•ln(2)
c = ln(8) = ln(23) = 3•ln(2)
Infine, si calcola l'espressione (a-c)/b:
La risposta corretta è, quindi, la a).
Quiz n. 15 (n. 60 Ragionamento Logico - Test Medicina Ufficiale anno accademico 2017-2018)
Traccia:
L'equazione di secondo grado kx2 – 3kx + (k+1) = 0, con k diverso da 0, ha una soluzione uguale a –1 per:
a) k = -1/5
b) k = -1
c) k = 1
d) k = 3
e) nessun valore di k
Risoluzione:
Si risolve l'equazione parametrica di II grado sostituendo nella traccia del quesito al posto della "x" la soluzione assegnata "-1"; tramite una semplice equazione di I grado si ricava, quindi, il valore incognito del parametro "k":
La risposta corretta è, quindi, la a).
TOLC MED 2024-25 - LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il TOLC MED 2024-25?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Torna alla pagina principale Test Medicina - facoltà statali