Test Bocconi - Matematica

: Scritto da Ing. Giovanni Galeone

Di seguito si riportano 10 esercizi svolti di Matematica utili per prepararsi al Test Bocconi.

Quiz n. 1

Traccia:

Ricercare le soluzioni della seguente disequazione logaritmica: log₃(4-x) < 2.

a) x < -5

b) x < -4 o x > 5

c) -5 < x < 4

d) x > -4

e) x > 4

Risoluzione:

La funzione logaritmo è definita per tutti i valori di x per i quali il suo argomento è positivo; bisogna quindi porre la seguente condizione di esistenza del logaritmo:

(1) 4 - x > 0

⇓

x < 4

Si risolve ora la disequazione applicando la definizione di logaritmo; inizialmente, poichè l'indice del logaritmo è maggiore di 1, non deve essere cambiato il verso della disequazione:

(2) log₃ (4-x) < 2

⇓

4 - x < 3²

⇓

4 - x < 9

⇓

x > -5

Mettendo a sistema i risultati ricavati dalle disequazioni (1) e (2), si ottengono le soluzioni richieste:

-5 < x < 4

La risposta corretta è, quindi, la c).

Quiz n. 2

Traccia:

La differenza attuale di età tra due fratelli è di 6 anni. Tra due anni il prodotto delle loro età varrà 216. Quali sono le età dei due fratelli oggi?

a) 12 e 18 anni

b) 8 e 14 anni

c) 14 e 20 anni

d) 10 e 16 anni

e) 12 e 16 anni

Risoluzione:

Si indicano con "x" e "y" le due età attuali incognite. Si "traduce" matematicamente la frase "La differenza attuale di età tra due fratelli è di 6 anni.":

(1) x - y = 6

⇓

x = y + 6

In maniera simile si "traduce" matematicamente la proposizione "Tra due anni il prodotto delle loro età varrà 216.":

(2) (x+2) • (y+2) = 216

Si sostituisce il valore di "x" ricavato dalla relazione (1) nella relazione (2) e si ottiene:

(y+8) • (y+2) = 216

⇓

y² + 10y - 200 = 0

⇓

y_1/2 = (-b ± √Δ) / 2a = (-10 ± 30) / 2

⇓

y₁ = -20 (non accettabile) e y₂ = 10

Sostituendo il valore di "y = 10" nella relazione (1), si ha:

x = 10 + 6 = 16

La risposta corretta è, quindi, la d).

Quiz n. 3

Traccia:

Determina l'equazione della parabola con asse parallelo all'asse y passante per (1;1) e avente vertice in (2;2).

a) y = -x²+4x-2

b) y = x²+3x-2

c) y = -x²+2x-4

d) y = -x²+4x

e) y = x²-3

Risoluzione:

L'equazione canonica di una parabola avente l'asse parallelo all'asse y è la seguente:

y = ax²+bx+c

Le coordinate del vertice di una parabola con asse parallelo all'asse y sono le seguenti:

x_v = (-b)/(2a); y_v = (-Δ)/(4a) (dove Δ = b² - 4ac)

Per ricavare i valori delle 3 incognite "a", "b" e "c", bisogna quindi imporre le seguenti 3 condizioni:

(1) (-b)/(2a) = 2

(il vertice ha ascissa assegnata pari a 2)

(2) (-Δ)/(4a) = 2

(il vertice ha ordinata assegnata pari a 2)

(3) 1 = a+b+c

[condizione di appartenenza del punto (1;1) alla parabola]

Dalla relazione (1), si ha:

b = -4a

Dalla relazione (3) si ha invece:

c = 1-a-b

⇓

c = 1+3a

Andando a sostituire i valori di "b" e "c" appena ottenuti nella relazione (2), si ricava "a":

(4ac - b²) / (4a) = 2

⇓

4a + 12a² - 16a² = 8a

⇓

4a² + 4a = 0

⇓

a = 0 (non accettabile perchè la parabola degenererebbe in una retta) e a = -1

Si possono infine calcolare i valore di "b" e "c":

b = -4a = (-4)•(-1) = 4

c = 1+3a = 1+(3)•(-1) = -2

Pertanto, l'equazione della parabola incognita è la seguente:

y = -x²+4x-2

La risposta corretta è, quindi, la a).

Quiz n. 4

Traccia:

La figura sottostante mostra un triangolo rettangolo; determina quale delle seguenti relazioni è corretta.

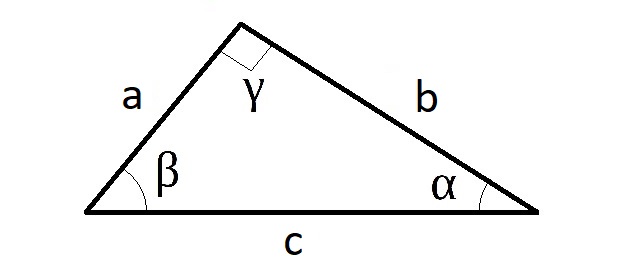
a) a = c•senβ

b) c = a•cotgβ

c) a = c•cosγ

d) b = c•cosα

e) b = c•tgβ

Risoluzione:

Si riportano di seguito i teoremi dei triangoli rettangoli, necessari per verificare la correttezza delle relazioni proposte dal quiz:

- Primo teorema sui triangoli rettangoli: in un triangolo rettangolo la misura di un cateto è data dal prodotto della misura dell'ipotenusa per il seno dell'angolo opposto;

- Secondo teorema sui triangoli rettangoli: in un triangolo rettangolo la misura di un cateto è data dal prodotto della misura dell'ipotenusa per il coseno dell'angolo acuto adiacente;

- Terzo teorema sui triangoli rettangoli: in un triangolo rettangolo la misura di un cateto è data dal prodotto della misura dell'altro cateto per la tangente dell'angolo opposto al primo;

- Quarto teorema sui triangoli rettangoli: in un triangolo rettangolo la misura di un cateto è data dal prodotto della misura dell'altro cateto per la cotangente dell'angolo adiacente al primo;

La risposta corretta è, quindi, la d): b = c•cosα.

Essa, infatti, è un esempio di corretta applicazione del secondo teorema sui triangoli rettangoli. Le relazioni contenute nelle altre alternative di risposta, invece, non costituiscono applicazioni corrette di nessuno dei quattro teoremi sui triangoli rettangoli.

Quiz n. 5

Traccia:

Determina le soluzioni della seguente equazione esponenziale:

2^x+3 - 3 = 4^x + 2^x+2

a) x=0 e x=-1

b) x=1 e x=log₃ (2)

c) x=-1 e x=4

d) x=0 e x=1/2

e) x=0 e x=log₂ (3)

Risoluzione:

Si risolve l'equazione esponenziale proposta:

2^x+3 - 3 = 4^x + 2^x+2

⇓

2^x•2³ - 3 = 2^2x + 2^x•2²

Per semplificare i calcoli, si utilizza ora l'incognita ausiliaria "y"; si continua pertanto a risolvere l'equazione esponenziale ponendo "2^x = y" e si ottiene:

8y - 3 = y² + 4y

⇓

y² - 4y + 3 = 0

⇓

y_1/2 = (-b ± √Δ) / 2a = (4 ± 2) / 2

⇓

y₁ = 1 e y₂ = 3

Sostituendo, nelle relazioni appena ottenute, "2^x" al posto di "y", si ha:

2^x = 1 ⇒ x = 0

2^x = 3 ⇒ x = log₂ (3)

La risposta corretta è, quindi, la e).

Quiz n. 6

Traccia:

Quanto vale l'area di un cerchio circoscritto ad un quadrato di lato "L"?

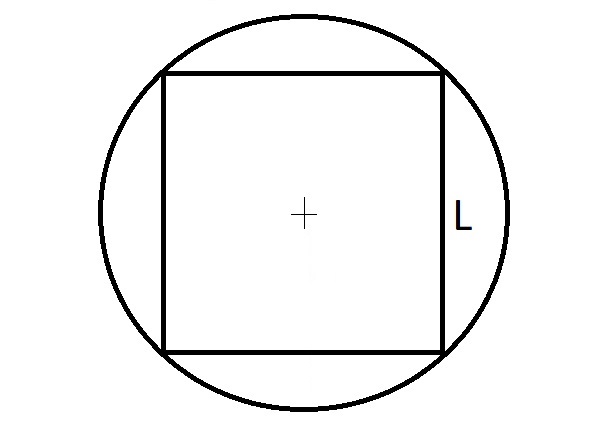
a) A = π•L²

b) A = (1/2)•π•L²

c) A = 2•π•L

d) A = (1/4)•π•L²

e) A = (3/2)•π•L²

Risoluzione:

L'area "A" di un cerchio di raggio "r" si calcola mediante la seguente formula:

A = π•r²

Nel caso in esame, il raggio del cerchio è uguale alla metà della diagonale del quadrato in esso inscritto. Pertanto, la diagonale del quadrato vale:

d = L√2

Si può, quindi, determinare il raggio del cerchio circoscritto al quadrato:

r = (L√2) / 2

Infine, si può ricavare l'area incognita del cerchio:

A = π•[(L√2)² / (2²)]

⇓

A = π•[(2L²) / 4]

⇓

A = (1/2)•π•L²

La risposta corretta è, quindi, la b).

Quiz n. 7

Traccia:

Una funzione è descritta dalla tabella sottostante:

Qual è la funzione?

a) f(x) = 5x+3

b) f(x) = 3^x-3

c) f(x) = x²+5x-3

d) f(x) = (x+8)/(x+2)

e) f(x) = x-3

Risoluzione:

Partendo dalle alternative di risposta, si verifica quale relazione sia verificata per tutti i valori di "x" e "f(x)" presenti in tabella:

- risposta a); si sostituiscono i valori di "x" e "f(x)" della tabella nella relazione f(x) = 5x + 3:

[-3 = 5•0 + 3] ⇒ [-3 = 3]

(prima riga della tabella non verificata)

- risposta b); si sostituiscono i valori di "x" e "f(x)" della tabella nella relazione f(x) = 3^x - 3:

[-3 = 3⁰ - 3] ⇒ [-3 = -3]

(prima riga della tabella verificata)

[3 = 3¹ - 3] ⇒ [3 = 0]

(seconda riga della tabella non verificata)

- risposta c); si sostituiscono i valori di "x" e "f(x)" della tabella nella relazione f(x) = x²+5x-3:

[-3 = 0² + 5•0 - 3] ⇒ [-3 = -3]

(prima riga della tabella verificata)

[3 = 1² + 5•1 - 3] ⇒ [3 = 3]

(seconda riga della tabella verificata)

[11 = 2² + 5•2 - 3] ⇒ [11 = 11]

(seconda riga della tabella verificata)

[21 = 3² + 5•3 - 3] ⇒ [21 = 21]

(seconda riga della tabella verificata)

La risposta corretta è, quindi, la c).

Quiz n. 8

Traccia:

La retta passante per il punto (-1, 3) e ortogonale alla retta di equazione 3x - y + 4 = 0 ha equazione:

a) 3x + y - 2 = 0

b) 3x + 3y + 8 = 0

c) x + 3y - 8 = 0

d) 3x - y + 6 = 0

e) x - 3y + 8 = 0

Risoluzione:

Si scrive dapprima il fascio di rette proprio di centro (-1, 3):

y - 3 = m•(x + 1)

Il coefficiente angolare incognito "m" deve essere l'antireciproco del coefficiente angolare della retta di equazione 3x - y + 4 = 0; infatti, per due rette perpendicolari di coefficienti angolari rispettivamente m ed m', vale la seguente relazione:

m = - (1/m')

Il coefficiente angolare della retta 3x - y + 4 = 0 vale:

m' = - a/b

⇓

m' = - 3/(-1) = 3

Si può, quindi, calcolare il coefficiente angolare "m":

m = - (1/m')

⇓

m = - (1/3) = -1/3

Sostituendo il valore di "m" ottenuto nel fascio proprio si ottiene l'equazione della retta incognita:

y - 3 = m•(x + 1)

⇓

y - 3 = (-1/3)•(x + 1)

⇓

3y - 9 = - x - 1

⇓

x + 3y - 8 = 0

La risposta corretta è, quindi, la c).

Quiz n. 9

Traccia:

Considera l'operazione a⊗b = (b-a) / (a+b). Allora l'operazione (2⊗5)⊗3 =

a) 3/4

b) -3/4

c) 4/3

d) 2/3

e) -4/3

Risoluzione:

Si esegue dapprima l'operazione 2⊗5:

2⊗5 = (5-2) / (2+5)

⇓

2⊗5 = 3/7

Successivamente, si effettua l'operazione (3/7)⊗3:

(3/7)⊗3 = [3-(3/7)] / [(3/7)+3]

⇓

(3/7)⊗3 = (18/7) / (24/7)

⇓

(3/7)⊗3 = 18/24

⇓

(3/7)⊗3 = 3/4

La risposta corretta è, quindi, la a).

Quiz n. 10

Traccia:

Si indica con PB(A) la probabilità che si verifichi l'evento A, sapendo che si è verificato l'evento B. Se P(B) = 4/7, P(A) = 2/7 e P(A∪B) = 9/14, quanto vale PB(A)?

a) 11/14

b) 7/8

c) 3/7

d) 5/8

e) 3/8

Risoluzione:

La formula per calcolare la probabilità condizionata PB(A) è la seguente:

PB(A) = [P(A) + P(B) - P(A∪B)] / P(B)

Applicando tale formula al caso in esame, si ha:

PB(A) = [(2/7) + (4/7) - (9/14)] / (4/7)

⇓

PB(A) = [(4+8-9) / 14] / (4/7)

⇓

PB(A) = 3/14 • 7/4

⇓

PB(A) = 3/8

La risposta corretta è, quindi, la e).

TUTOR QUALIFICATO ON-LINE

Ti stai preparando per il Test Bocconi?

Affidati alla professionalità e all'esperienza...prenota ora il tuo corso di preparazione online, via Skype, con l'Ing. Galeone.

Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!

Per maggiori info clicca QUI.