In questa pagina si riportano 15 quiz svolti di Matematica presenti nei Test Professioni Sanitarie Ufficiali degli scorsi anni.
Quiz n. 1
Traccia:
Quale delle seguenti equazioni rappresenta la retta passante per l'origine degli assi e per il punto (6; 3)?
a) y = x
b) y = 2x
c) y = (1/2)x
d) y = x-3
e) y = 3x+3
Risoluzione:
In geometria analitica, l'equazione di una retta passante per l'origine degli assi cartesiani è:
dove con "m" si indica il coefficiente angolare della retta; si possono quindi scartare le risposte d) ed e), perchè aventi equazioni esprimibili nella forma y = mx+q.
Poichè la retta incognita deve passare anche per il punto (6;3), è possibile ricavare il valore di "m" sostituendo nell'equazione della retta le coordinate del punto stesso (x = 6 e y = 3):
⇓
m = 3/6
⇓
m = 1/2
L'equazione della retta è quindi:
La risposta corretta è, quindi, la c).
Quiz n. 2
Traccia:
L'equazione x2 + 49 = 0 ha soluzioni:
a) x1 = x2 = 7
b) x1 = 7; x2 = -7
c) non reali
d) reali
e) x1 = x2 = -7
Risoluzione:
Si risolve l'equazione di II grado pura:
⇓
x2 = -49
L'equazione non ammette soluzioni reali, perchè il quadrato di un qualsiasi numero reale deve essere necessariamente maggiore o uguale a zero.
La risposta corretta è, quindi, la c).
Quiz n. 3
Traccia:
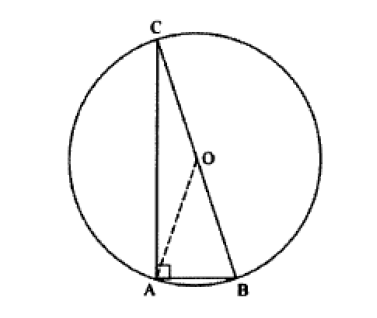
Sapendo che l'angolo AOB misura 50°, quanto misura l'angolo ABC?
a) 50°
b) 25°
c) 90°
d) 155°
e) 65°
Risoluzione:
Si nota immediatamente che il triangolo AOB è isoscele, in quanto i lati AO e BO, essendo raggi della stessa circonferenza, sono uguali; ne consegue che anche gli angoli alla base OAB e OBA sono uguali.
Conoscendo quindi l'angolo al vertice AOB (50°) e, sapendo che la somma degli angoli interni in un triangolo è sempre 180°, si può calcolare l'ampiezza di ciascuno dei due angoli alla base:
⇓
OAB = OBA = 130°/2
⇓
OAB = OBA = 65°
Poichè l'angolo OBA coincide con l'angolo incognito ABC, si deduce che la risposta corretta è la e).
Quiz n. 4
Traccia:
In una scatola ci sono dieci palline nere, una pallina rossa e una verde. Qual è la probabilità, pescandone due a caso, che si tratti della pallina rossa e di quella verde?
a) (1/12)(1/12)
b) (1/12)(1/11)
c) 2/12
d) (2/12)(1/11)
e) 2/10
Risoluzione:
La probabilità che alla prima estrazione si peschi una pallina rossa o verde è 2/12, perchè si hanno una pallina rossa e una verde su un totale di 12 palline.
Alla seconda estrazione la probabilità di pescare la pallina rimasta (rossa o verde che sia) è 1/11, perchè sarà rimasta una sola pallina rossa o verde su un totale di 11 palline (una pallina non va contata perchè pescata nella precedente estrazione).
La probabilità totale è data dal prodotto delle probabilità dei due eventi appena calcolate:
La risposta corretta è, quindi, la d).
Quiz n. 5
Traccia:
Giovanni e Andrea camminano l'uno verso l'altro, lungo un marciapiede rettilineo, e la loro distanza iniziale è di 600 metri: Giovanni procede a 6 km/h e Andrea a 4 km/h. Quanto distano i due uomini l’uno dall’altro quando mancano 3 minuti al loro incontro?
a) 50 m
b) 200 m
c) 500 m
d) 150 m
e) 400 m
Risoluzione:
Se Giovanni procede a 6 km/h, è possibile conoscere la distanza che egli percorre in 3 minuti tramite la proporzione:
⇓
x = (6000 • 3 ) / 60
⇓
x = 300 m
Con una proporzione simile, si va a ricercare la distanza percorsa da Andrea (che procede a 4 km/h) in 3 minuti:
⇓
x = (4000 • 3) / 60
⇓
x = 200 m
Poichè i ragazzi camminano l'uno verso l'altro, le due distanze appena trovate, vanno sommate:
La risposta corretta è, quindi, la c).
Quiz n. 6
Traccia:
Le diagonali di un esagono sono:
a) 12
b) 6
c) 9
d) 3
e) 18
Risoluzione:
Il numero di diagonali che si possono tracciare in un poligono di n lati è dato da:
Applicando tale formula al caso in esame, si ha:
⇓
d = 9
La risposta corretta è, quindi, la c).
Quiz n. 7
Traccia:
Se sen(x) = 2/3 e 90° < x < 180°, allora sen(2x) vale:
a) 4/3
b) -(4√5)/9
c) -(2√5)/9
d) -(2√5)/3
e) -1/9
Risoluzione: si utilizza innanzitutto la prima relazione fondamentale della trigonometria:
Applicando la relazione precedente, si ricava infatti il cos(x):
⇓
cos (x) = √[1 - 4/9]
⇓
cos (x) = √(5/9)
⇓
cos (x) = -√5/3
(il coseno nel secondo quadrante è negativo)
Successivamente, dalla formula di duplicazione del seno si ha:
⇓
sen(2x) = 2•(2/3)•(-√5/3)
⇓
sen(2x) = -(4√5)/9
La risposta corretta è, quindi, la b).
Quiz n. 8
Traccia:
Se il logaritmo in base 9 di x è -3 allora:
a) x = 1/729
b) x = 729
c) l'equazione non ha senso perchè il valore di un logaritmo non può mai essere negativo
d) x = 1/3
e) l'equazione non ha senso perchè la base è maggiore di 1
Risoluzione:
Si "traduce" matematicamente la traccia del quiz:
Per la definizione di logaritmo si ha che la base (9) elevata al logaritmo (-3) deve essere uguale all'argomento del logaritmo (x); si ha quindi:
↓
x = 1/93
↓
x = 1/729
La risposta corretta è, quindi, la a).
Quiz n. 9
Traccia:
Quanti sono i modi distinti di realizzare un poker d’assi (4 assi e 1 carta diversa) scegliendo in un mazzo di 52 carte da gioco? (L’ordine di scelta delle carte non ha importanza)
a) 52
b) 26
c) 4
d) 13
e) 48
Risoluzione:
In questo caso non è necessario utilizzare formule di calcolo combinatorio: i quattro assi vanno presi sempre tutti.
Le carte rimanenti sono 48 e, quindi, 48 sono i possibili modi di realizzare un poker d'assi.
Pertanto, la risposta corretta è la e).
Quiz n. 10
Traccia:
Due sfere hanno raggi di lunghezza l’una tripla dell’altra. Qual è il rapporto tra la misura del volume della sfera di raggio maggiore e quella del volume della sfera di raggio minore?
a) 2π
b) 27
c) 3π
d) 9
e) π
Risoluzione:
La formula per calcolare il volume di una sfera è la seguente:
Dalla formula sopra indicata, si deduce che il volume di una sfera cresce proporzionalmente al cubo del suo raggio, quindi se il rapporto tra i raggi delle due sfere vale 3, il rapporto tra i rispettivi volumi vale 33 = 27.
La risposta corretta è, quindi, la b).
Quiz n. 11
Traccia:
Un triangolo rettangolo ha l’ipotenusa uguale a 25 cm. I suoi cateti misurano:
a) 15 cm e 20 cm
b) 7 cm e 20 cm
c) 5 cm e 25 cm
d) 9 cm e 16 cm
e) 14 cm e 15 cm
Risoluzione:
I tre lati di un triangolo rettangolo devono soddisfare il teorema di Pitagora (la somma dei quadrati dei due cateti deve essere uguale al quadrato dell'ipotenusa):
Secondo la formula sopra indicata, le misure dei 3 lati del triangolo devono costituire una terna pitagorica.
La risposta corretta è perciò la a), infatti si ha:
Quiz n. 12
Traccia:
La somma 2,1·104 + 3,5·103 dà come risultato:
a) 5,6·107
b) 2,45·107
c) 5,6·104
d) 24,5·103
e) 5,6·1012
Risoluzione:
Il primo addendo della somma può essere riscritto nel seguente modo:
E' ora possibile effettuare la somma dei numeri (indicati nella traccia con la notazione esponenziale) raccogliendo a fattor comune:
La risposta corretta è, quindi, la d).
Quiz n. 13
Traccia:
Dalle prime 10 rilevazioni è risultato che il peso delle studentesse di una scuola è in media pari a 60 kg. Le successive 15 rilevazioni danno un peso medio pari a 55 kg. Qual è il peso medio delle 25 studentesse?
a) 58 kg
b) 57,5 kg
c) 57 kg
d) 56 kg
e) 55 kg
Risoluzione:
E' possibile risolvere il quiz applicando la formula della media aritmetica ponderata; indicando con "x" i valori (nel caso in esame i pesi medi) e con "f" le frequenze (nel caso in esame il numero di rilevazioni), si ha:
⇓
M = (60•10 + 55•15) / (10 + 15)
⇓
M = 1425 / 25
⇓
M = 57 kg
La risposta corretta è, quindi, la c).
Quiz n. 14
Traccia:
Siano a un numero reale maggiore di 1 e b un numero reale positivo minore di 1; allora il prodotto ab è:
a) non ci sono dati sufficienti per rispondere
b) minore di a e maggiore di b
c) maggiore di a e minore di b
d) maggiore di a e di b
e) minore di a e di b
Risoluzione:
Poichè l'enunciato indicato nella traccia deve essere sempre vero, si considerino 2 numeri reali con le caratteristiche richieste, ad esempio a = 2 e b = 1/2.
In questo caso il loro prodotto vale: ab = 2•(1/2) = 1.
Il prodotto ab è minore di a e maggiore di b.
La risposta corretta è, quindi, la b).
Quiz n. 15
Traccia:
Le soluzioni della disequazione x2 – 3x > 4 sono:
a) x < –1, x > 4
b) x < 0, x > 3
c) nessuna delle altre risposte è corretta
d) x < –3
e) nessuna soluzione
Risoluzione:
Portando a primo membro tutti i termini della disequazione di II grado assegnata, si ha:
Successivamente si risolve l'equazione di II grado associata:
⇓
Δ = b2 - 4ac = 32 - 4•1•(-4) = 9 + 16 = 25
⇓
x1/2 = (-b ± √Δ) / 2a = (3 ± 5) / 2
⇓
x1 = -1 e x2 = 4
Quando il segno del coefficiente del termine di secondo grado in "x" è concorde con il verso della disequazione (entrambi maggiori di zero) le soluzioni corrispondono ai valori esterni:
La risposta corretta è, quindi, la a).
LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il Test di ammissione alla Facoltà di Professioni Sanitarie?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Per tornare alla pagina principale - Test Professioni Sanitarie - clicca QUI.