In questa pagina si riportano 10 quiz svolti di Logica presenti, negli scorsi anni, nei test di ammissione ufficiali alle Facoltà di Ingegneria in diversi atenei d'Italia.
Quiz n. 1
Traccia:
Dobbiamo dimostrare che un certo numero x è inferiore ad un altro numero y diverso da x. Quante fra le seguenti affermazioni permettono di dedurre la nostra tesi? (1) esiste un numero compreso tra di loro; (2) ogni numero non superiore a x è minore di y; (3) tutti i numeri sono inferiori a y o superiori a x; (4) nessun numero supera y e non supera x.
a) 3
b) 1
c) 4
d) 2
e) 0
Risoluzione:
L'ipotesi (1) non permette di dedurre necessariamente la tesi, infatti potrebbe essere valida la relazione y < x e quindi esistere un numero tra x ed y superiore a y ed inferiore a x.
Anche le ipotesi (3) e (4) non danno nessuna informazione esplicita sulla posizione relativa dei numeri x ed y sull'asse dei numeri reali (o di qualsiasi altro insieme numerico) e quindi non escludono che y sia minore a x.
La proposizione (2), "ogni numero non superiore a x è minore di y", può essere tradotta in simboli matematici nel seguente modo:
⇓
n < y
Inoltre, essendo x diverso da y, si deduce necessariamente che:
(come indica la tesi)
La risposta corretta è, quindi, la b).
Quiz n. 2
Traccia:
Sia data la seguente sequenza di ottagoni:
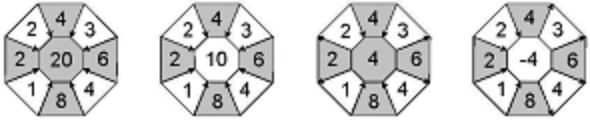
Quale dei seguenti ottagoni è coerente con la regola deducibile dagli ottagoni soprastanti?

a) l'ottagono 3
b) l'ottagono 2
c) l'ottagono 4
d) l'ottagono 5
e) l'ottagono 1
Ottagono 1:
Ottagono 2:
Ottagono 3:
Ottagono 4:
Seguendo gli stessi criteri logico-matematici la risposta corretta è, quindi, la c), ossia l'ottagono 4:
Quiz n. 3
Traccia:
Alla fine dei 6 incontri di un torneo all’italiana di tennis fra 4 amici è risultato che tutti hanno perso almeno un incontro e tutti hanno vinto almeno un incontro. Quale fra le seguenti affermazioni può essere dedotta?
a) tutti e quattro hanno vinto due incontri
b) non abbiamo elementi sufficienti per poter trarre queste conclusioni
c) esattamente tre persone hanno vinto due incontri
d) esattamente due persone hanno vinto due incontri
e) una sola persona ha vinto due incontri fra i tre disputati
Risoluzione:
Si indicano i tennisti rispettivamente con le lettere A, B, C e D si ipotizzano 6 risultati per le partite del girone rispettando il vincolo richiesto dalla traccia: "ogni tennista ha perso almento un incontro e vinto almeno un incontro":
A batte C
B batte C
B batte D
C batte D
D batte A
Si effettua quindi un riepilogo delle partite vinte e perse dai 4 tennisti:
B (2 vinte; 1 persa)
C (1 vinta; 2 perse)
D (1 vinta; 2 perse)
La risposta corretta è, quindi, la d): esattamente due persone hanno vinto due incontri.
Quiz n. 4
Traccia:
Dire quale delle seguenti coppie di numeri continua la successione: 3-17; 5-16; 9-14; 17-11; 33-7; ?-?
a) 51 e 2
b) 65 e 3
c) 51 e 3
d) 15 e 1
e) 65 e 2
Risoluzione:
I primi numeri di ogni coppia sono legati tra loro secondo il seguente criterio:
sommato ad incrementi che aumentano sempre del doppio)
Nella prosecuzione della serie si avrà quindi:
I secondi numeri di ogni coppia, invece, sono legati nel seguente modo:
che lo precede quantità che aumentano sempre di una unità)
Continuando la serie si avrà:
La risposta corretta è, quindi, la e).
Quiz n. 5
Traccia:
Ad un pranzo di sei persone ogni partecipante conosce almeno altri due convitati e, prima di iniziare, presenta fra di loro ogni coppia di suoi conoscenti, se già non si conoscono. Quando si siedono, si conoscono tutti fra di loro. Perciò:
a) tutti i convitati ne conoscevano almeno tre
b) l’avvenimento descritto non è possibile
c) ogni convitato ne conosceva esattamente due
d) uno dei convitati conosceva tutti
e) almeno uno dei convitati ne conosceva almeno altri tre
Risoluzione:
La traccia chiede una condizione necessaria al fatto che tutti si conoscano nel momento in cui si siedono.
Per le risposte a), b) e c) si trovano dei controesempi in cui si verifica l'ipotesi ma non la tesi, e quindi sono false.
La risposta corretta è la e), infatti si possono fare le seguenti considerazioni:
- se si considera l'invitato A, egli conosce almeno B e C.
- affinché D, E ed F arrivino a conoscere A, si possono presentare 2 scenari: a) lo conoscevano prima di iniziare il pranzo, e quindi A conosceva almeno tre invitati (B, C e almeno uno tra D, E, F); b) si sono conosciuti al pranzo attraverso le presentazioni di B o C, ma in quest'ultimo caso B o C conosceva almeno tre invitati (A e almeno due tra D, E, F).
In definitiva, almeno uno dei convitati ne conosceva almeno altri tre.
Quiz n. 6
Traccia:
Giocando a Risiko Giulio Cesare ha vinto più di suo nipote Augusto, ma non di Napoleone. Alessandro Magno ha vinto meno di Carlo Magno, ma non più di Napoleone. Chi ha vinto meno?
a) Carlo Magno
b) Alessandro Magno
c) Napoleone
d) Augusto
e) Giulio Cesare
Risoluzione:
Dalla prima proposizione si ricava che:
Dalla seconda proposizione si deduce invece che:
In conclusione, la risposta corretta è la d):
Quiz n. 7
Traccia:
La frase "Sul tavolo ci sono due bicchieri" implica che sul tavolo:
a) ci sono due bicchieri e una bottiglia
b) non ci sono bottiglie
c) ci sono due bicchieri e due tazzine di caffè
d) c'è un bicchiere
e) non ci sono tre bicchieri
Risoluzione:
Le risposte a), b) e c) non sono necessariamente vere, perchè non viene data alcuna informazione sulla presenza o meno di bottiglie e di tazzine di caffè sul tavolo.
Anche la risposta e) non è corretta perchè la frase iniziale non specifica che ci sono SOLO due bicchieri, quindi nulla esclude che ce ne possa essere un terzo.
La risposta corretta è quindi la d), infatti se sul tavolo vi sono due bicchieri, è possibile affermare con assoluta certezza che sul tavolo c'è almeno un bicchiere.
Quiz n. 8
Traccia:
Per numerare le pagine di un libro sono state usate in totale 3300 cifre. Le pagine del libro sono:
a) tra 1500 e 2000
b) tra 2000 e 3000
c) meno di 1000
d) più di 3000
e) tra 1000 e 1500
Risoluzione:
Da pagina 1 a pagina 9 si devono usare 10 cifre.
Da pag. 10 a pag. 99 si hanno 90 numeri, tutti con due cifre ciascuno; quindi in totale si utilizzano 90•2 = 180 cifre.
Da pag. 100 a pag. 999 si hanno 900 numeri, tutti con tre cifre ciascuno; in totale si usano perciò 900•3 = 2700 cifre.
Da pag. 1000 a pag. 1149 si hanno 150 numeri da quattro cifre ciascuno per un totale di 150•4 = 600 cifre.
Sommando le diverse quantità ottenute si ha:
Si è abbondantemente superata la soglia di 3300 cifre ricercate, quindi la risposta corretta è la e):
Quiz n. 9
Traccia:
Al termine della seduta di allenamento della Nazionale, Totti e Buffon fanno la seguente scommessa: Totti tirerà 12 rigori e Buffon cercherà di pararli. Per ogni rigore parato Totti darà 50 euro a Buffon mentre per ogni rigore segnato Buffon darà 40 euro a Totti. Dopo di ciò viene eseguita la serie di rigori al termine della quale Totti deve ricevere da Buffon 120 euro. Quanti rigori ha parato Buffon?
a) 9
b) 5
c) 6
d) 4
e) 12
Risoluzione:
Si indicano con "RP" i rigori parati e con "RS" i rigori segnati; deve valere la prima relazione:
Inoltre il prezzo pagato da Totti a Buffon per tutti i rigori parati dal portiere si può indicare con 50•RP, mentre il prezzo pagato da Buffon a Totti per tutti i rigori segnati dall'attaccante si indica con 40•RS. Poichè alla fine della serie dei 12 rigori, Totti deve ricevere da Buffon 120 euro, la differenza tra il denaro guadagnato da Totti (40•RS) e quello guadagnato da Buffon (50•RP) deve essere proprio pari a 120 euro; si può pertanto esplicitare la seconda relazione:
Si tratta quindi di risolvere un sistema lineare di 2 equazioni in 2 incognite.
Dalla prima relazione si può ricavare RS:
Sostituendo il valore di RS appena calcolato nella seconda relazione si ha:
⇓
90 • RP = 360
⇓
RP = 4
⇓
RS = 8
Buffon ha parato 4 rigori e Totti ne ha segnati 8.
La risposta corretta è, quindi, la d).
Quiz n. 10
Traccia:
Di una famiglia si sa che: 1) almeno un maschio non è celibe; 2) tutti i laureati sono celibi; 3) non è vero che almeno un maschio non è maggiorenne. Solo una delle seguenti proposizioni è deducibile dalle premesse. Quale?
a) nessun maggiorenne non è coniugato
b) tutti i celibi sono laureati
c) almeno un maggiorenne è coniugato
d) almeno un celibe non è maggiorenne
e) almeno un maggiorenne non è coniugato
Risoluzione:
Parafrasando le tre proposizioni si sa che:
1) almeno un maschio è coniugato;
2) tutti i laureati sono celibi;
3) tutti i maschi sono maggiorenni.
Dalle premesse 1) e 3) si può dedurre che almeno un maggiorenne è coniugato.
La risposta corretta è, quindi, la c).
LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il Test di ammissione alla Facoltà di Ingegneria?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!